新闻资讯

机械设计：什么是刚体?刚体模型与质点模型的区别与联系

　　

　　本文来源：力学酒吧公众号(ID：Mechanics-Bar)，作者：张伟伟 太原科技大学。

　　什么是刚体?刚体模型与质点模型两者都是理想化模型。

　　刚体是指在运动中和受力作用后，形状和大小不变，而且内部各点的相对位置不变的物体。刚体模型和质点模型的区别如下：

　　1、定义不同

　　刚体是指在运动中和受力作用后，形状和大小不变，而且内部各点的相对位置不变的物体;

　　质点模型，是用一个具有同样质量，但没有大小和形状的点来代替实际物体，这是对实际物体的一种科学抽象。

　　2、类别不同

　　刚体模型是物体;质点模型是一种抽象表达。

　　3、存在形式不同

　　绝对刚体实际上是不存在的，只是一种理想模型，因为任何物体在受力作用后，都或多或少地变形，如果变形的程度相对于物体本身几何尺寸来说极为微小，在研究物体运动时变形就可以忽略不计;

　　质点模型只是对实际物体的一种科学抽象，是不存在的。

　　4.质点和刚体区别在它们的自由度上，点在空间只可能产生x，y，z三个方向的线位移，因此我们说质点有3个自由度;而对于刚体除了x，y，z三个方向的线位移外，还可以产生绕x，y，z三个轴的转动，也成为角位移，因此我们称刚体有6个自由度。

　　举例来说，研究人造卫星的飞行轨迹，可以不考虑人造卫星的形状和大小，将卫星简化为质点来处理，它的位置可以用经度、维度和高度3个量来描述(即3个自由度)。假如在卫星上安装一台照相机，要对地面、或太空进行拍照，那么卫星的姿态就显得比较重要了。此时仅用经度、维度和高度3个量描述卫星就不足以说明拍照对象和角度，除此3个量之外，还需要对卫星进行姿态描述。

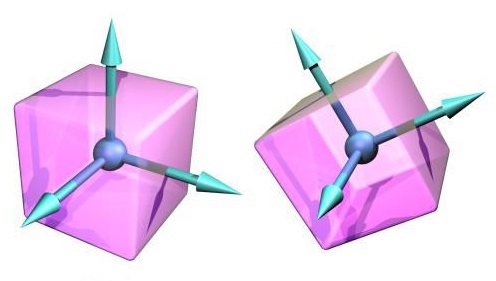
　　欧拉 (Leonhard Euler，1707-1783) 最早 (1760年) 用进动角、章动角和自转角(合称欧拉角)描述了刚体在三维欧氏族空间的绕定点运动。考虑下图所示蓝色坐标系x，y，z为参考坐标系，红色坐标系X，Y，Z是固定在刚体上，随刚体一起运动，称之为随动坐标系。因此，认为红色坐标系的运动就代表了刚体的运动。

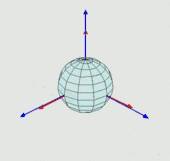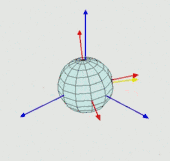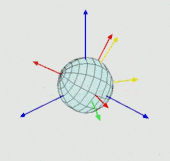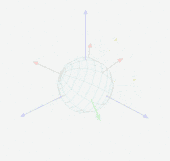
　　请与下图对应着看

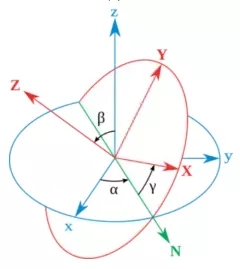
　　假如红色坐标系的初始状态与参考坐标系重合(可配合动图理解)，认为刚体运动可分解为三个步骤：

　　红色坐标系绕oz轴(与oZ轴重合)旋转α 角度，称为进动角，此时oX轴转至oN位置处;

　　绕红色坐标系oN轴(即新的oX轴)旋转β角度，称为章动角，这样oN垂直于zoZ平面的，称oN为节线;

　　再绕新的oZ轴旋转γ角度，称为自转角。如果通过节线可以比较清楚的定义三个角：

　　(1) 节线oN与参考坐标系ox轴的夹角为进动角α;

　　(2) 随动坐标系oZ轴与参考坐标系oz轴的夹角为章动角β;

　　(3) 随动坐标系oX轴与节线oN的夹角为自转角γ。

　　进动角 (Precession)、章动角 (nutation)、自转角 (intrinsic rotation) 是来自天文学的三个概念。我们以地球的运动来说明：例如地球绕自转轴旋转(下图中绿色R标示)，由此产生的角度就是自转角;其次，由于地球在绕太阳公转的同时还受到月球的吸引力，称月球绕地球的旋转平面为白道面，而地球绕太阳的旋转为赤道面，由于赤道和白道之间有5o的差距，因此月球会对地球产生一个扭转作用，致使地球在绕太阳公转的方向上左右摇摆(下图中红色N标示)，像是向太阳点头一般，由此产生的角度改变称为章动角;最后地球在高速自转时，当外力产生的力矩矢与自转轴不重合时就会产生进动，这种运动导致自转角看起来像是在做圆锥摆动(下图中蓝色P标示，陀螺运动中经常会见到进动)。

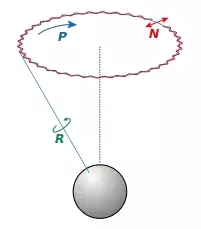
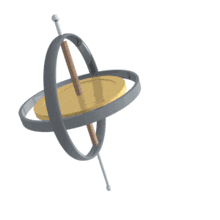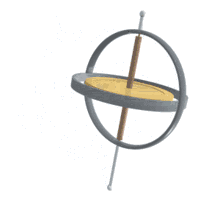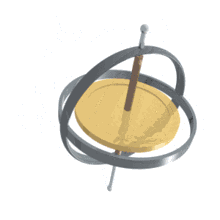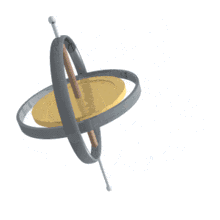
　　这种运动就是进动

　　在航天器中，进动角α，章动角β 和自转角γ 通常称为描述刚体的姿态角，在有的资料中α，β，γ也用ψ，θ，φ来表示。对于飞行中的飞机，其姿态调整通常采用偏航 (yaw)，仰角 (pitch) 和滚动 (roll) 来描述(如下图所示)，它们也是欧拉角的一种。值得一提的是欧拉角并不是唯一的，选择不同旋转轴和转动顺序，可以产生24种不同的广义欧拉角。

偏航/yaw

仰俯/pitch

滚动/roll

　　在理论力学上，欧拉角被用来描述刚体定点运动，将刚体的任意运动分解为定点(质心)的空间运动和刚体的定点运动合成，定点所代表的运动被称为平动(物体上任何一点都具有和定点相同的运动)，然后再利用欧拉角描述刚体的绕定点运动。

　　在刚体的学习中，很多质点的结论可推广应用到刚体中。从静力学角度考虑，一维情况下限制一个质点的运动，只需要在该方向上施加约束(或力);在二维平面内，需要2个约束(或力);再到三维空间则需要3个约束(或力)。如果对于刚体，一维情况下不需要考虑刚体转动，只有该方向上的运动，此时刚体与质点情况一样;在二维平面内，除2个方向上的约束外，还需要1个限制刚体旋转的约束(或力偶);在三维空间内，就需要3个方向上的约束，加3个限制刚体旋转的约束(或力偶)。如果把旋转看作是一种广义位移，力偶看作是广义力，从建立控制方程上，刚体和质点没有本质上的区别，只是方程数量增加，求解问题的复杂程度增加。

　　在这些结论在动力学中，也同样适用。质点的动力学方程用牛顿第二定律表示为：

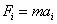
　　这里i 为1、2、3对应于x、y、z轴。对于刚体动力学问题，可分解为质心的动力学方程加刚体定点运动的动力学方程，成为：

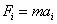
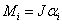
　　这里i 仍为1、2、3对应于x、y、z轴，M 表示力偶，α 是角加速度，下标i 表示绕某轴的力偶或角加速度。J 被称为转动惯量，表达式是

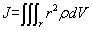
　　式中，r 表示微元体ρdm到转动轴的距离。在质点模型中，质量m 是衡量物体惯性大小的量，质量大，惯性就大，就更倾向于保持原运动状态。

　　在刚体转动中，转动惯量J 就是衡量刚体发生转动惯性大小的量，转动惯量大，转动惯性就大，表明保持原转动特性的能力大。换言之，质量m 是表征线位移上惯性大小的指标，而转动惯量是表征角位移上惯性大小的指标。实际上，描述刚体的转动时，将描述质点的质量换成转动惯量，将施加于质点的集中力换成力偶，质点动力学的大多数结论在刚体转动中仍然成立。

　　在质点动力学中，将刚体转动的J、M、α 视为广义的m、F、a，质点动力学的许多结论可以适用于刚体转动。例如质点平衡与刚体转动平衡，动量定理与动量矩定义，能量守恒定律，冲量定律等等。尽管刚体与质点有这么多的相似，刚体力学的发展要晚质点力学许多，牛顿作为经典力学的奠基人仍不会求解刚体问题，到1760年(牛顿的《自然哲学的数学原理》成书于1687年)欧拉给出了欧拉角描述刚体的绕定点运动，到1765年发表《刚体运动理论》将刚体的运动分解为刚体上一点的运动与刚体绕该点的定点运动。但欧拉解决的是单个刚体的运动情况，对于由刚体组成的刚体系统问题则要借助1788年拉格朗日的《分析力学》，1834年哈密顿又将其推广到了哈密顿力学(分析力学的另一种体系)。到20世纪，人们又开始关心运动的稳定性问题，由此引发了非线性动力系统的非线性特征和系统控制理论研究，直到今天，仍然是动力学系统研究的热点问题之一。