新闻资讯

解析力学力矩和力偶矩的正负

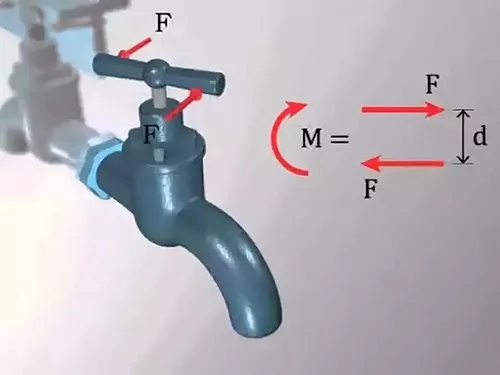
一、力矩的正负

对于初次接触力矩概念的学生，判断力矩正负有一定的认知挑战性(对于教师或已掌握的自是“会者不难”)，这需要通过形象的例子缩小认知梯度。

力矩的正负需要从物体的定轴转动谈起。

物体定轴转动可以用圆盘在其平面内转动表示。为了表示圆盘的运动状态，除了要知道转动快慢之外，我们还需要知道转动的转向。显然转向只有两个状态，一个是逆指针(图1a),另一个是顺时针(图1b)。

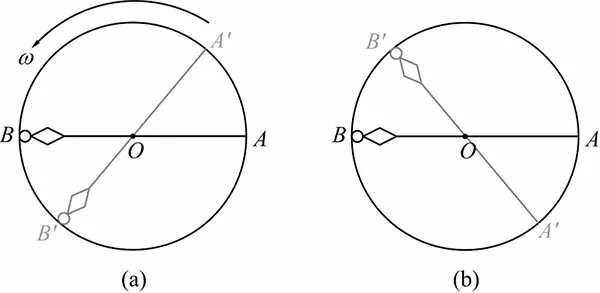
图1

对只有两个状态的物理量，自然可以用正号和负号来区分。通常选择逆时针为正，顺时针为负(这种选法与空间情形的右手螺旋法则一致)。按此选法，一个带正负号的量就既能表示定轴转动的快慢，也能表示圆盘转向了。

如果圆盘转向为逆时针(正号)，某个力有使转动加速的效果，那么这个力对转轴之矩就是正的。反之，如果该力使逆时针转动的圆盘减速，则此力对转轴之矩就是负的。

力可以通过使物体获得加速度来体会，但是为了使研究结果有一般性，我们往往尽可能只讨论力(暂时把物体放到一边去)。对力矩也是这样，即使没有物体，我们也能讨论力矩。

物体既然没有了，转动轴当然也就不存在。此时，为了表征力的转动效果，我们是计算力对矩心之矩—可以把这个矩心形象地想象为定轴转动的轴。

想象在矩心处有一垂直于纸面的轴(见图2)，伸出右手，让大拇指沿轴方向，四指卷曲去抓住这根轴。如果力的作用顺着上述四指从指根到指尖，则该力对矩心的矩为正，比如图中的F1。

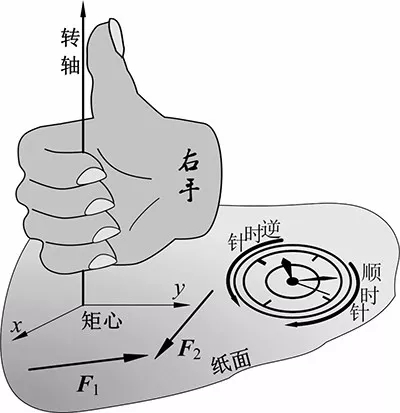
图2

若想象纸面上有个闹钟，则上述四指从指根到指尖卷曲的转向与钟的逆时针转向一致，这就是逆时针转向的矩为正的原因。反之，如果力对矩心的作用与四指从指根到指尖卷曲转向相反，如图中的F2,则该力对矩心的矩为负，对应的转向为顺时针转向。

如果还是没感觉，那么从力矢的尾端向始端画个弧，矩心要被这个弧和力矢包含在内。如果从力尾端到力始端的弧是逆时针的，则该力对矩心的矩是正的，否则为负。见图3。

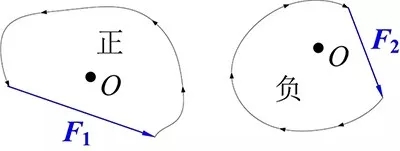
图3

二、力偶矩的正负

力偶可以理解为两个力来配对，配对条件是它们大小相等，方向相反。力偶矩的正负号当然要与力矩的一致，即“顺时针为负，逆时针为正”规则，也可用图2来示意。若无示意图时，当然就使用这个规则，如M=40 N·m表示逆时针转向的力矩，大小为40 N·m，而M=-30 N·m表示顺时针转向的力矩，大小为30 N·m。

力学分析喜欢使用受力图。一旦有受力图，总是把图形示意的转向为参考转向，比如图4中四个带箭头的弧标明了参考转向，弧箭头旁边的符号M1,M2,M3,M4表示力矩的数值，它要另行补充，比如 M1=10 N·m , M2=-20 N·m, M=30 N·m, M=-40 N·m。

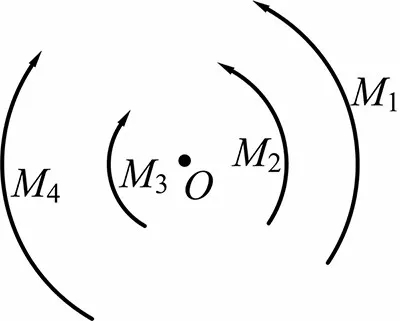
图4

M1=10 N·m的数值与图示的弧箭头转向一起表示这是大小为10 N·m的逆时针转向力偶。也不能因M2=-20 N·m中有负号而认为它是顺时针转向，而是因为有了图形，M2数值和图示转向一起表明是大小为20N·m顺时针转向作用的力偶。M=30 N·m也不表示它是逆时针，参考图示转向，它是大小为30 N·m的顺时针转向作用的力偶。类似地，M=-40 N·m与图示参考转向一起，表示大小为40 N·m的逆时针转向作用的力偶。

三、写平衡方程

在写矩平衡方程时，我们会选择一个参考正转向(如无明确声明，则默认逆时针为参考正转向)。参考受力图，如果力对矩心的转动作用与参考正转向一致则在方程中为正号，反之，当力对矩心的转动作用与参考正转向相反，该力的矩在平衡方程中取负号。

对不同的矩心，力矩的正负号可能会变。

力偶处理与上述力矩类似，但是正负号(和大小都)不因矩心而变。

参考文献

来源：图形公式不烦恼公众号（ID：ArtByMathematica），作者：陈奎孚。 .理论力学精细辅导.北京：清华大学出版社.2018.9