新闻资讯
数控编程:教学数控宏程序编程,这里有窍门

数控宏程序编程,是用变量的方式进行数控编程的方法。数控宏程序分为A类和B类宏程序,其中A类宏程序比较老,编写起来也比较费时费力,B类宏程序类似于C语言的编程,编写起来也很方便。不论是A类还B类宏程序,它们运行的效果都是一样的。一般说来,华中的数控机床用的是B类宏程序,广州数控机床用的是A类宏程序。想成为编程工程师,掌握手工高级编程宏程序是一个基本功。学会宏程序编程,你的编程水平就会提升一个境界!
但是许多师傅感觉数控宏程序编程非常的难,其实当你找到窍门之后,你会发现非常简单。
今天用案例来教大家编写一个宏程序的关键思路:变量关系式的推理。
我们知道不管是软件编程,还是手工编程,对一个程序而言无外乎有两大部分组成:
1,G指令。
2,点位坐标。
数控G指令,常用的就那么几十个,寥寥数几,但是零件不论是直线,圆弧,还是曲线曲面,它都是由无数个小点组成的,然后点与点之间用小线段连接起来,从而构成了形形色色的产品。
那么编程的时候,若这些点位的数据处理非常多,那么加工出来的零件轮廓就光滑。
比如下图,在一箱体上有几处孔,要在数控加工中心上面加工内孔和孔底圆弧(红色圈的部位)。
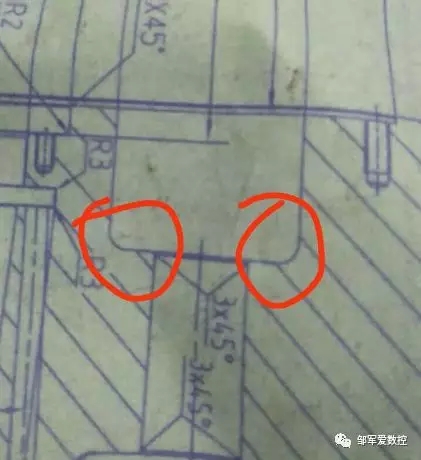
孔底圆弧的加工非常好处理,搞个带R的铣刀和零件圆弧R一样即可,采用螺旋插补铣,包括孔底面的不平整都能做出来。这样程序就非常简单。
军哥之前分享过螺旋插补铣孔宏程序,在这直接上程序。
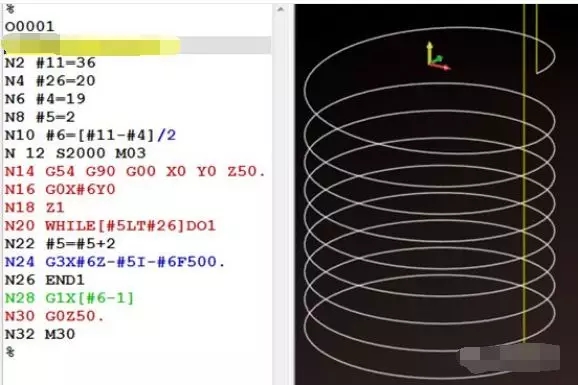
但问题来了,几处孔底的圆弧R不一样, 能不能螺旋插补铣完孔之后,让程序一次性铣出圆弧R来?这样也没接刀痕。

若你懂宏程序编程就非常简单啦。程序精简,更重要的是程序通用性好,一个程序满足任何孔的加工。
那么如何来编写宏程序呢?
今天就给大家分享一招编写宏程序的核心思路:变量关系式的推理
比如下面是圆弧R放大简图:
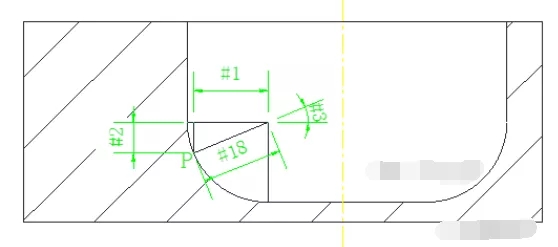
你还记得军哥上面说的:零件都是由小数点组成,然后点与点之间用小线段连接起来, 若这些点位的数据处理非常密集,那么加工出来的零件轮廓就光滑。
如上图,设P为圆弧上的任一点,采用变量的方式推算出P点的坐标值。
如何推导求出P点坐标? 利用数学上的三角函数即可。
关于三角函数,在一个直角三角形中,角和边会存在关系,如下图所示:
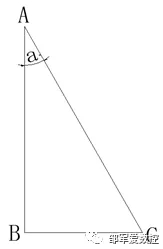
假设已知∠a的度数和AB边的长,要求出BC、AC的边长该怎么来求?
根据已知条件,可以得出以下几个角与边的公式:
sin a=BC/AC cos a=AB/AC tan a=BC/AB
根据上述公式,可以很容易算出BC、AC的边长。比如求AC边长。根据公式cosa=AB/AC 可以推算出AC=AB/cosa
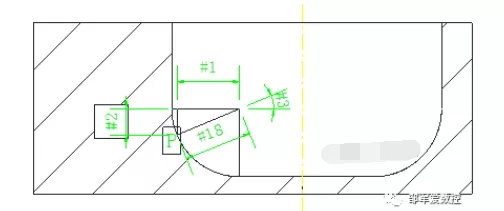
那么在圆弧中做一个直角三角形,如上图所示。
根据三角函数公式,可以得出下关系式:
#1=#18*COS[#3] ( X )
#2=#18*SIN[#3] ( Z )
有了关系式,需要知道#18和#3 才能求出#1和#2。
1,关于#18
#18代表要加工的圆弧R,属于已知数值,比如图纸要加工R5.1 那么
可以给#18赋值5.1,即#18=5.1
2,关于#3
#3代表夹角,加工过程中,角度#3是逐渐变化的,也就P点从0度逐渐增加到90度。角度逐渐递增,比如#3=#3+5,后面加的数值越小,那么P点越密集,编写的程序加工出的圆弧越光滑。
好了,知道#18和#3这两个数据,我们就计算出了#1(X方向数值)和#2(Z方向数据)。
程序如下:
…….
#3=0
#18=5.1
WHILE[#3LT90]DO1
#1=#18*COS[#3]
#2=#18*SIN[#3]
…….
加工圆弧程序
…….
#3=#3+1
END1
%
说明:
1,角度变量#3=0开始,当#3小于90就一直循环WHILE与END之间程序段,也就是一直循环加工【圆弧程序段】。
2,通过变量#3的自增运算,当变量#3的数值超过90,就结束循环,也就是圆弧加工完毕。
那么加工圆弧的程序如何编写呢?
计算出的#1和#2是以加工的圆弧R为中心,编程的时候大多以孔为中心,零件表面为Z的零点。
那么还需要进一步推导出以编程原点为基准的关系式。
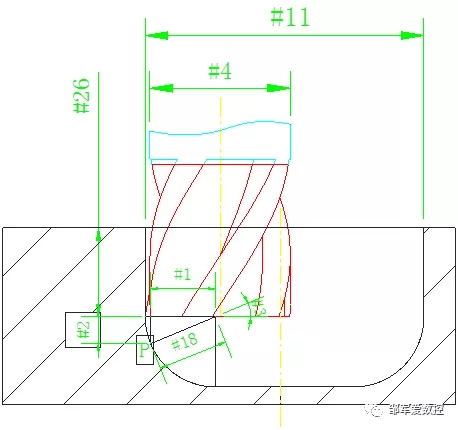
设#11为孔直径,#4为刀具直径,#26为孔深,如上图所示。
#24=[#11-#4]/2
那么P点
X方向:[#24-#1]
Z方向: [#26+#2]
变量之间的关系式就这么推导了出来,有了关系式,加工圆弧的程序就非常简单了。
G01X[#24-#1]F30
Z-[#26+#2]
G03I[#24+#1]
有了关键的程序段,直接复制上面讲过的程序结构。
程序如下:
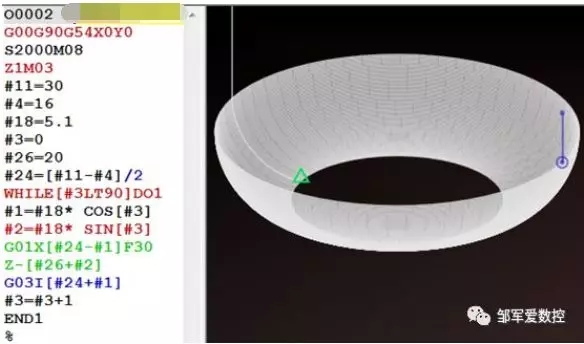
好了,案例就不再过多分析了。
因为军哥曾经强调:案例不重要,思路很重要,编程方法很重要,你用心回顾下,军哥是如何一步一步推出变量之间的关系式的。
其实宏程序里面应用了大量的编程技巧,比如数学模型的建立,变量关系式的推导,加工刀具的选择,走刀方式的取舍等等,这些都是一个合格的编程工程师所要具备的基本功。